중학교 1학년에서는 다음과 같이 구의 부피와 겉넓이를 구하는 방법을 배워요.
반지름이 $r$인 구에 대해 그것의 부피는 $\frac{4}{3}\pi r^3$이며, 겉넓이는 $4\pi r^2$이다.
교과서에서는 이것에 대한 수학적 증명 대신 물을 이용해 실험적으로 부피를 구하여 이것이 공식의 값과 매우 근사함을 보여요. 하지만 이런 증명은 전혀 수학적이지 않지요. 이번에는 중학교 수준에서 구의 부피와 겉넓이를 구하는 방법을 알아볼 거예요.
핵심 아이디어. 카발리에리의 원리
두 평행선 $l$과 $m$이 있고 두 꼭짓점은 $l$ 위에, 다른 한 꼭짓점은 $m$ 위에 있는 삼각형 $\triangle \mathrm{ABC}$를 생각해봐요.

이제 직선 $l$, $m$은 가만히 두고 $\mathrm{A}$를 움직여봐요. 이렇게 만들어지는 모든 삼각형은 원래의 삼각형과 넓이가 같아요.

둘의 넓이가 같은 이유는 삼각형의 넓이를 구하는 공식에서 밑변의 길이와 높이가 같기 때문이라고 할 수 도 있겠지만 다르게 한번 봐볼게요.
$l$과 $m$ 사이의 또 다른 평행선 $k$에 대해 $\triangle \mathrm{ABC}$ 안에 있는 $k$의 길이와 $\triangle \mathrm{A^{\prime}BC}$ 안에 있는 $k$의 길이는 같아요. 그러니 아래 그림에서 $\mathrm{\overline{XY}}=\mathrm{\overline{X^{\prime}Y^{\prime}}}$이라는 거예요.

이 사실은 두 삼각형이 $\mathrm{\overline{BC}}$를 공통으로 가지고 있고 $\mathrm{\overline{XY}}$와 $\mathrm{\overline{X^{\prime}Y^{\prime}}}$까지 같은 닮음비를 가지고 있음에서 간단히 증명돼요. 그러니 $l$과 $m$ 사이 임의의 직선에 대해 두 도형이 그 직선을 지나는 길이는 같음을 확인할 수 있어요.
그런데 평면도형을 수없이 많은 선분의 쌓임으로 생각해봐요. 같은 높이에서 같은 길이를 가지는 두 도형은 넓이가 같은가요? 그렇겠죠. 이것이 카발리에리의 원리예요. 어떤 직선과 그 직선과 평행한 직선으로 두 도형을 자를 때 같은 직선에 대해 각각의 도형을 지나는 선분의 길이가 같으면 두 도형의 넓이는 같아요. 이걸 공간으로 확장하면 구의 부피를 정확히 구하는 데 사용할 수 있어요.
구의 부피를 구해보자!

자 이렇게 오른쪽에 반지름이 $r$인 구를, 왼쪽에는 원기둥을 딱 맞는 원뿔 모양으로 자른 입체를 놓아볼게요. 원기둥의 밑면은 반지름이 $r$인 원이고, 높이는 $r$이에요. 이렇게 하면 원기둥의 밑면이 속하는 평면과 평행한 모든 평면에 대해 왼쪽 입체와 오른쪽 입체가 각각 지나는 부분의 넓이는 같아요. 이것은 다음과 같이 증명할 수 있어요.
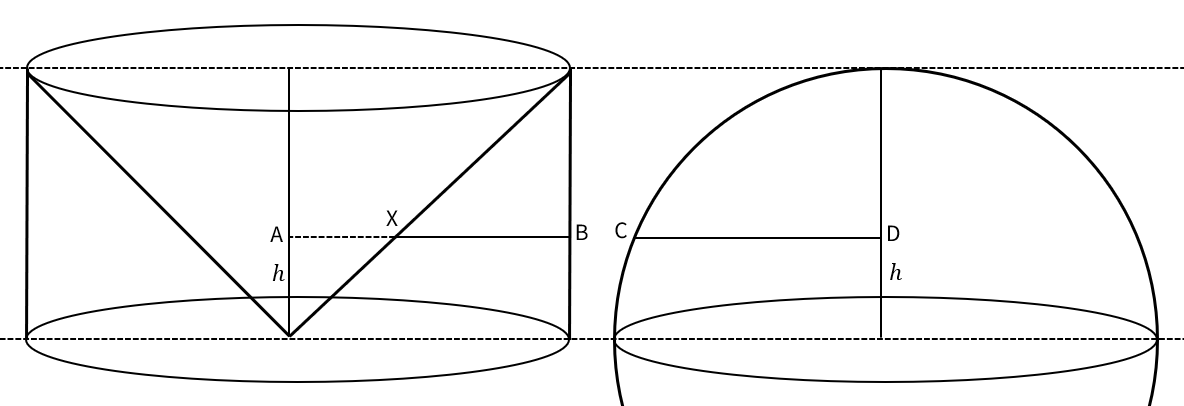
우선 반구의 부피를 구하는데 집중해요. 어차피 나중에 2배 하면 되니까요. 밑면에서 $h$만큼 떨어진 평면으로 두 입체를 잘랐을 때 왼쪽은 도넛 모양으로, 오른쪽은 원 모양으로 잘릴 것이에요.
왼쪽 입체에서 잘린 평면의 넓이는 다음과 같이 구해요.
$\mathrm{\overline{AX}}=h$이겠죠. 이것은 이 입체의 원기둥 반지름과 높이가 같기 때문이에요. 그리고 $\mathrm{\overline{AB}}=r$이에요. 그림으로 그려보면 다음과 같아요.
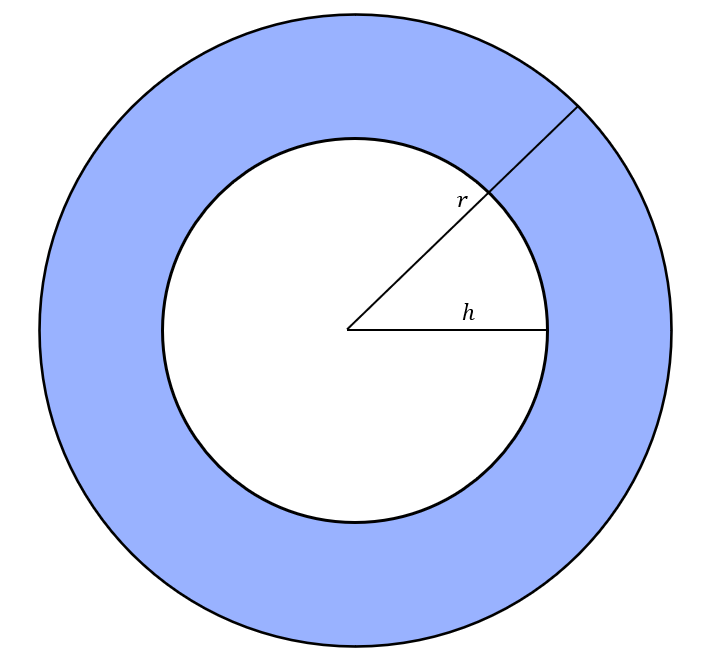
구하고자 하는 넓이는 파란색으로 색칠한 부분이니 다음과 같이 구할 수 있겠죠.
$\pi r^2 - \pi h^2 = \pi(r^2 - h^2)$
구에서는 다음과 같이 구할 수 있어요.
C와 D, 그리고 구의 중심을 꼭짓점으로 가지는 삼각형은 D가 직각인 직각삼각형이에요. 빗변의 길이가 $r$이고 또 다른 한 변이 $h$이므로 피타고라스의 정리에 의해 $\mathrm{\overline{AX}}^2=r^2 - h^2$이에요. 따라서 단면의 넓이는 다음과 같아요.
$\pi\mathrm{\overline{AX}}^2=\pi( r^2 - h^2)$
이렇게 임의의 높이 $h$에 대해 두 단면의 넓이가 같은 것이 증명되었으니, 앞선 카발리에리의 원리에 의해 두 입체의 부피가 같은 게 증명되었어요. 이제 구의 부피 대신 왼쪽의 조금은 익숙한 입체의 부피를 대신 구할 수 있지요. 원기둥을 원뿔이 빼는 입체의 부피는 다음과 같이 구해요.
$\left( \pi r^2 \right)\left(r\right)-\frac{1}{3}\left( \pi r^2 \right)\left(r\right)=\frac{2}{3}\pi r^3$
따라서 반지름이 $r$인 반구의 부피는 $\frac{2}{3}\pi r^3$이에요. 온전한 구는 이것의 2배인
$\frac{4}{3}\pi r^3$
이겠지요.
구의 겉넓이 구하기
이제 구의 겉넓이를 구하는 방법에 대해 생각해볼게요. 우선 뿔의 부피를 구하는 방법을 분명히 할게요. 밑면의 모양과 상관 없이 밑면의 넓이가 $S$, 높이가 $h$인 뿔의 부피는 다음과 같아요.
$\frac{1}{3}Sh$
이제 구를 다음과 같이 수없이 많은 뿔로 나누어볼게요.
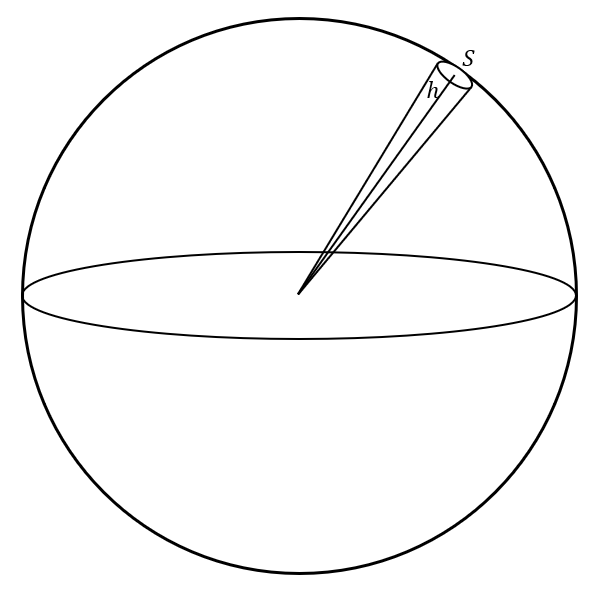
각 뿔의 밑면은 $S$이고 높이는 $h$인데 $h=r$이에요. 그럼 이 수없이 많은 뿔의 부피 합은 다음과 같을거에요.
$\sum{\left(\frac{1}{3}Sr\right)}=\frac{r}{3}\sum{S}$
그런데 앞서 구를 빈틈없이 뿔로 채웠다고 했지요. 따라서 각 뿔의 부피 합은 구의 부피와 같아야 해요.
$\frac{r}{3}\sum{S}=\frac{4}{3}\pi r^3$
식을 정리하면 밑면 넓이의 합인 $\sum{S}$는 다음과 같이 표현되요.
$\sum{S}=4 \pi r^2$
그런데 밑면 넓이의 합이 겉넓이와 같겠죠? 따라서 이것이 구의 겉넓이가 되는거에요.
$4\pi r^2$
이 방법은 수학적으로 엄밀한가요?
아니요 앞선 방법도 엄밀히 따지면 수학적으로 엄밀하다고 할 수 없어요. 당장 뿔의 부피가 기둥의 1/3 임을 설명해야, 카발리에리의 원리가 성립함을 증명해야, 구를 수없이 많은 뿔로 쪼갤 수 있음을 보여야 이러한 정리를 사용할 수 있어요. 그리고 이 과정에는 (거의 확실히) 미적분학이 들어가죠. 하지만 구의 부피를 이런 방법으로 구할 수도 있음을 설명하는데 앞선 설명은 의의가 있겠죠!
'수학 > 기하' 카테고리의 다른 글
| 물체의 충돌로 원주율 근사하기 (0) | 2021.09.05 |
|---|---|
| 제1, 2 코사인정리 (0) | 2021.08.24 |
| 삼각형의 넓이를 구하는 8가지 방법 (2) | 2021.07.16 |
