가장 먼저 고려해야 할 것은 "물체가 멀어지면서 어떻게 보일까?"이다.
우리는 경험적으로 멀리 있는 물체는 작게 보임을 안다. 물론 가까이서 보면 크게 보인다.
하지만 정확히 얼마나 크고, 얼마나 작게 보일까?
멀리 볼수록 얼마나 넓게 볼 수 있을까?
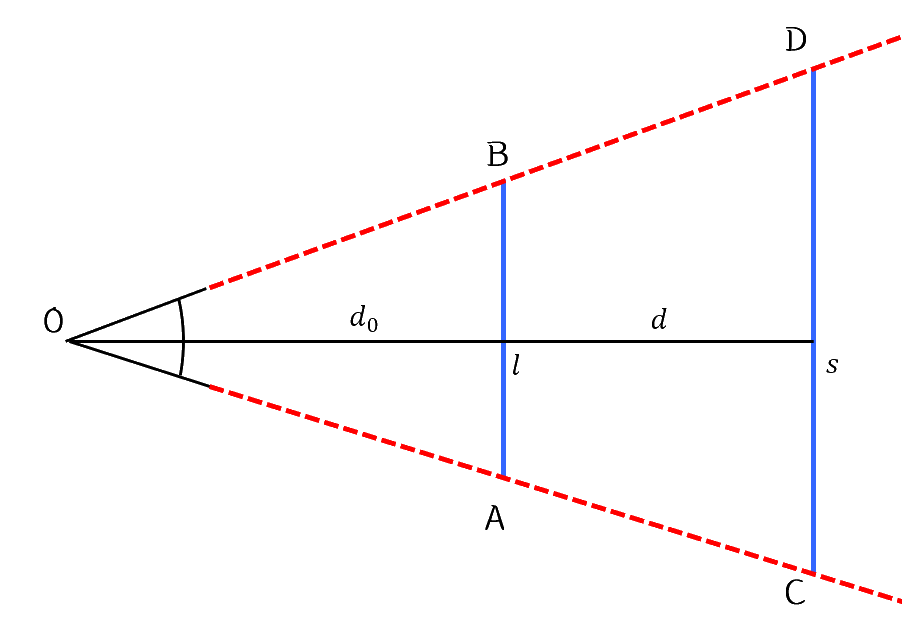
위 이미지는 2차원 세상에서 눈이 볼 수 있는 시야를 나타낸 것이다.
눈은 빨간색 점선 안의 것을 볼 수 있으며, 그 바깥의 것은 시야에서 벗어나기 때문에 볼 수 없다.
파란색 선들은 특정한 거리에서 눈이 볼 수 있는 최대 시야를 나타낸 것이다. 가령 눈에서 $d_0$만큼 떨어진 곳에서는 $l$만큼의 시야를 가진다.
이때 삼각형의 닮음을 사용하면 $l$과 $s$ 사이의 관계를 알 수 있다.
$\mathrm{\triangle OAB \sim \triangle OCD\;(AA)}$
$\therefore\;d_0:l=(d_0+d):s$
$s=\frac{l(d+d_0)}{d_0}$$=\left(\frac{d}{d_0}+1\right)l$
이제 시야 속의 물체가 어떤 크기로 보일지 생각해보자.
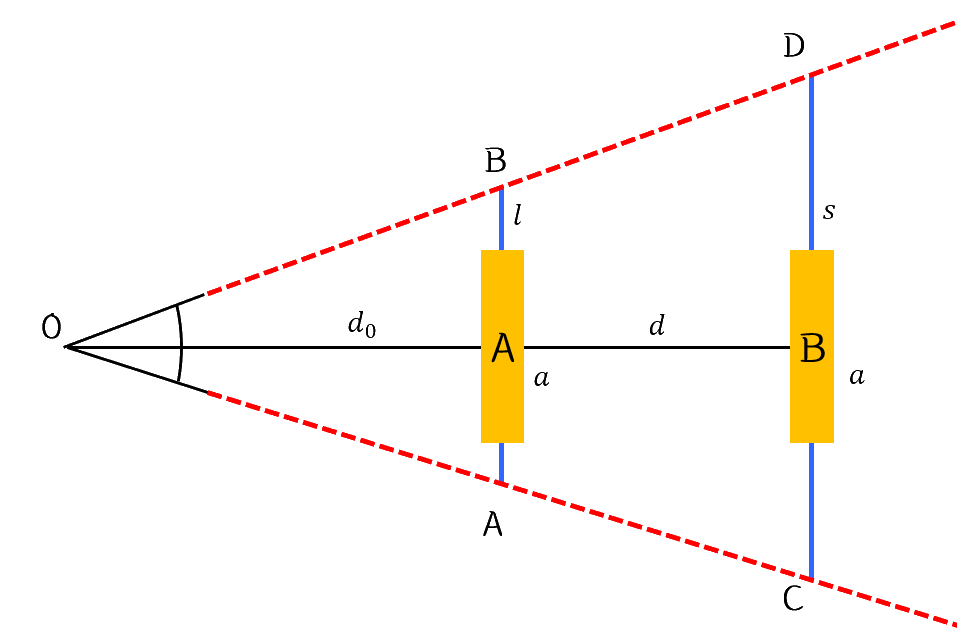
위 그림은 두 시야에서 크기가 같은 두 물체 A와 물체 B가 있는 모습이다.
우리는 경험적으로 A와 B는 절대적인 크기는 같지만 다른 크기로 보임을 안다. 시야가 넓든 좁든 우리는 같은 크기로 인지하기 때문이다. 따라서 더 이상 절대적인 크기는 중요하지 않다. 물체가 시야에서 차지하는 상대적인 비율(이하 시야 차지율)을 따질 것이다.
예를 들어 시야 차지율이 0.6인 물체는 시야 차지율이 0.2인 물체의 3배로 보인다. 시야 차지율은 얼마나 멀리 보고 있는지, 시야는 얼마나 넓은지에 상관없이 물체가 얼마나 크게 보이는지 상대적으로 비교해준다.
위 그림에서 물체 A의 시야 차지율은 다음과 같다.
$\frac{a}{l}$
같은 이치로 물체 B의 시야 차지율은 다음과 같다.
$\frac{a}{s}$
여기에 앞서 밝혀낸 $s$와 $l$의 관계를 대입하면 물체 B의 시야 차지율은 다음과 같다.
$\frac{a}{\frac{l(d+d_0)}{d_0}}$$=\frac{ad_0}{l(d+d_0)}$
두 물체의 시야 차지율을 비교해보면 B는 A의
$\frac{d_0l}{l(d+d_0)}$$=\frac{d_0}{d+d_0}$
배다.
그러니 어떤 눈에서 $d$만큼 떨어진 물체를 $l$만큼 뒤로 보내면 크기는 $\frac{d}{d+l}$배가 된다.
한번 이 사실로 실험을 해보자.
실험 목표
앞서 세운 "거리에 따른 물체 크기 변화 공식"이 현실에서 잘 맞아떨어지는지 확인한다.
실험 과정
- 자를 수평면에 두고, 0mm 지점에 카메라를 설치한다.
- 동전의 위치를 50mm, 100mm, 150mm, 200mm 등 바꾸어 가며 카메라로 사진을 찍는다.
- 사진에 찍힌 동전의 크기를 비교한다.
실험 결과
| 카메라-동전 거리(mm) | 50.0 | 100.0 | 150.0 | 200.0 |
| 동전 크기 | 1.00 | 0.546 | 0.378 | 0.288 |
동전의 크기는 50.0mm에서를 1로 잡은 상댓값이다.
실험값과 이론값을 비교해보자.
50.0mm 기준 이론값과 오차
| 카메라-동전 거리(mm) | 50.0 | 100.0 | 150.0 | 200.0 |
| 실험값 | 1.00 | 0.546 | 0.378 | 0.288 |
| 이론값 | 1.00 | 0.500 | 0.333 | 0.250 |
| 오차 | 0.000 | -0.092 | -0.134 | -0.152 |
동전이 멀수록 오차가 커지긴 하지만, 그럭저럭 맞는 모습이다. 더 많은 테스트 케이스를 통해 이론을 검증해보자.

이번에는 거리를 50.0mm에서 290.0mm까지 늘려가며 20.0mm마다 측정을 했다.
그 결과가 왼쪽 그래프이다. 보다시피 실험값과 이론값이 거의 맞아떨어지는 것을 볼 수 있다. 평균 오차는 -0.12이다.
오차는 대부분이 실험기구의 한계인 듯하다. 자가 카메라의 일직선상에 놓이지 않았거나, 동전이 기울어져 있었다거나 하는 문제가 있었을 수 있다.
구현
Java 이미지 프로세싱 라이브러리 중에는 이미지 리사이즈 메서드가 있어서 크기 바꾸기는 어렵지 않게 구현할 수 있다.
우선 이미지를 리사이즈하는 메서드를 만들자.
public BufferedImage resize(BufferedImage in, int width, int height) {
Image tmp = in.getScaledInstance(width, height, Image.SCALE_SMOOTH);
BufferedImage nImg = new BufferedImage(width, height, BufferedImage.TYPE_INT_ARGB);
Graphics2D g2d = nImg.createGraphics();
g2d.drawImage(tmp, 0, 0, null);
g2d.dispose();
return nImg;
}그리고 이 메서드로 물체를 앞뒤로 이동시킨 이미지를 만드는 메서드를 만들자.
public BufferedImage moveFrontBack(BufferedImage in, double current, double distance) {
double diff = current / (distance + current);
return resize(in, round(diff*in.getWidth()), round(diff*in.getHeight()));
}diff 값을 구하는 과정에서 앞서 구한 공식이 들어간다. 이제 이렇게 얻은 이미지를 그래픽으로 뿌려주면 된다.
이때 Java 그래픽은 왼쪽 위 좌표를 입력하도록 되어있지만, 우리는 이미지가 가운데를 중심으로 움직였으면 좋겠기 때문에 이미지의 가운데 좌표를 입력하면 왼쪽 위 좌표로 변형하는 메서드가 필요하다.
public Pair<Integer, Integer> moveLocationCenter(Pair<Integer, Integer> pos, int width, int height) {
pos.first(pos.first()-width/2);
pos.second(pos.second()-height/2);
return pos;
}이미지의 가운데 좌표에 이미지 너비의 절반, 높이의 절반을 빼서 구현된다. 이제 그래픽 라이브러리로 화면에 뿌려주자.
...
BufferedImage bi = ImageIO.read(new File("sand.png"));
bi = imageProcessor.resize(bi, 400, 400);
bi = imageProcessor.moveFrontBack(bi, 1.0, distance);
Image image = bi;
Pair<Integer, Integer> pos = new Pair<>(width/2, height/2);
pos = moveLocationCenter(pos, bi.getWidth(), bi.getHeight());
g.drawImage(image, pos.first(), pos.second(), this);
...마지막으로 distance 변숫값을 변화시키는 키 입력 트리거를 설정해준다.
private class Control implements KeyListener {
@Override
public void keyTyped(KeyEvent e) {}
@Override
public void keyPressed(KeyEvent e) {
if(e.getKeyCode() == KeyEvent.VK_W) {
distance+=0.1;
}
else if(e.getKeyCode() == KeyEvent.VK_S) {
distance-=0.1;
}
repaint();
}
@Override
public void keyReleased(KeyEvent e) {}
}W키가 눌리면 거리를 늘리고, S키가 눌리면 거리를 줄인다.
이제 실행해보자.
이번 글에서는 물체의 거리가 멀어짐에 따라 어느 정도로 크기가 바뀌는지 수학적
으로 생각해보고, 실험을 통해 그 결론을 검증했고, 컴퓨터 시뮬레이션으로 제작해봤다.
이제 우리는 물체를 자유자재로 멀리 둘 수 있고, 가깝게 둘 수도 있다
'이것저것 > 3차원을 2차원으로 옮기기' 카테고리의 다른 글
| 3차원을 2차원으로 옮기기 - Abstract (0) | 2021.10.11 |
|---|
