2D Transform
앞선 글에서 WebGL을 사용하여 도형을 그리는 방법을 알아봤어요. 이제 이 도형을 필요에 따라 변형하는 방법을 알아볼 거예요.
변형(Transform)은 다음과 같이 3가지가 있어요.
- Translation (평행이동)
- Scaling (크기 조정)
- Rotation (회전)
이번에는 코드를 먼저 전부 올릴게요.
<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8">
</head>
<body>
<p>WebGL</p>
<canvas id="canvas" width="800" height="600"></canvas>
</body>
<script>
var dx=200, dy=100, sx=1, sy=1, angle=0;
const pi = Math.PI;
var g;
function initWebGL() {
const canvas = document.getElementById('canvas');
const gl = canvas.getContext('webgl');
g = gl;
if(!gl) {
console.log("WebGL을 사용할 수 없습니다.");
}
const vertexShaderSource = document.getElementById("vertex-shader").text;
const fragmentShaderSource = document.getElementById("fragment-shader").text;
const vertexShader = createShader(gl, gl.VERTEX_SHADER, vertexShaderSource);
const fragmentShader = createShader(gl, gl.FRAGMENT_SHADER, fragmentShaderSource);
const program = createProgram(gl, vertexShader, fragmentShader);
const positionAttributeLocation = gl.getAttribLocation(program, "a_position");
var resolutionLocation = gl.getUniformLocation(program, "u_resolution");
const transformUniformLocation = gl.getUniformLocation(program, "transform");
const positionBuffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, positionBuffer);
var positions = [
0, 0,
30, 0,
0, 150,
0, 150,
30, 0,
30, 150,
30, 0,
100, 0,
30, 30,
30, 30,
100, 0,
100, 30,
30, 60,
67, 60,
30, 90,
30, 90,
67, 60,
67, 90,
];
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(positions), gl.STATIC_DRAW);
render = () => {
gl.viewport(0, 0, gl.canvas.width, gl.canvas.height);
// Clear the canvas
gl.clear(gl.COLOR_BUFFER_BIT);
gl.useProgram(program);
gl.enableVertexAttribArray(positionAttributeLocation);
gl.bindBuffer(gl.ARRAY_BUFFER, positionBuffer);
var size = 2;
var type = gl.FLOAT;
var normalize = false;
var stride = 0;
var offset = 0;
gl.vertexAttribPointer(positionAttributeLocation, size, type, normalize, stride, offset);
gl.uniform2f(resolutionLocation, gl.canvas.width, gl.canvas.height);
const translateMatrix = transform.translate(dx, dy);
const scaleMatrix = transform.scale(sx, sy);
const rotateMatrix = transform.rotate(angle);
const transformMatrix = m3.multiply(m3.multiply(translateMatrix, rotateMatrix), scaleMatrix);
gl.uniformMatrix3fv(transformUniformLocation, false, transformMatrix);
var primitiveType = gl.TRIANGLES;
var offset = 0;
var count = 18;
gl.drawArrays(primitiveType, offset, count);
}
render();
}
window.onload = initWebGL;
function createShader(gl, type, source) {
const shader = gl.createShader(type);
gl.shaderSource(shader, source);
gl.compileShader(shader);
var success = gl.getShaderParameter(shader, gl.COMPILE_STATUS);
if(success) return shader;
console.log(gl.getShaderInfoLog(shader));
gl.deleteShader(shader);
}
function createProgram(gl, vertexShader, fragmentShader) {
const program = gl.createProgram();
gl.attachShader(program, vertexShader);
gl.attachShader(program, fragmentShader);
gl.linkProgram(program);
const success = gl.getProgramParameter(program, gl.LINK_STATUS);
if (success) {
return program;
}
console.log(gl.getProgramInfoLog(program));
gl.deleteProgram(program);
}
</script>
<script id="vertex-shader" type="glsl">
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 transform;
void main() {
vec2 position = (transform * vec3(a_position, 1)).xy;
vec2 clipSpace = ((position / u_resolution) * 2.0)-1.0;
gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
}
</script>
<script id="fragment-shader" type="glsl">
precision mediump float;
void main() {
gl_FragColor = vec4(0.12, 0.12, 0.12, 1);
}
</script>
<style>
canvas {
width: 800px;
height: 600px;
border: 1px solid #000;
}
</style>
<script>
/**
* 평행 이동 행렬을 만듭니다.
* @param{number} dx x축 평형 이동
* @param{number} dy y축 평행 이동
* @return{Array.number} 평행 이동 행렬
*/
translate = function(dx, dy) {
return [
1, 0, 0,
0, 1, 0,
dx, dy, 1
];
}
/**
* 크기 조정 행렬을 만듭니다.
* @param{number} sx x축 크기 배율
* @param{number} sy y축 크기 배율
* @return{Array.number} 크기 조정 행렬
*/
scale = function(sx, sy) {
return [
sx, 0, 0,
0, sy, 0,
0, 0, 1
]
}
/**
* 기준점을 가진 크기 조정 행렬을 만듭니다.
* @param{number} sx x축 크기 배율
* @param{number} sy y축 크기 배율
* @param{number} originX 기준점의 x 좌표
* @param{number} originY 기준점의 y 좌표
* @return{Array.number} 크기 조정 행렬
*/
scaleOrigin = function(sx, sy, originX, originY) {
return [
sx, 0, 0,
0, sy, 0,
-originX*(sx-1), -originY*(sy-1), 1
]
}
/**
* 회전 변환 행렬을 만듭니다.
* @param{number} angle 반시계방향을 +로 하는 회전 각도(radian)
* @return{Array.number} 회전 변환 행렬
*/
rotate = function(angle) {
const s = Math.sin(angle), c = Math.cos(angle);
return [
c, s, 0,
-s, c, 0,
0, 0, 1
];
}
/**
* 축을 가진회전 변환 행렬을 만듭니다.
* @param{number} angle 반시계방향을 +로 하는 회전 각도(radian)
* @param{number} originX 기준점의 x 좌표
* @param{number} originY 기준점의 y 좌표
* @return{Array.number} 회전 변환 행렬
*/
rotateOrigin = function(angle, originX, originY) {
const s = Math.sin(angle), c = Math.cos(angle);
return [
c, s, 0,
-s, c, 0,
-originX*(c-1)+originY*s, -originX*s-originY*(c-1), 1
]
}
const transform = {
translate: translate,
scale: scale,
scaleOrigin: scaleOrigin,
rotate: rotate,
rotateOrigin: rotateOrigin
}
</script>
<script>
var m3 = {
multiply: function(a, b) {
var a00 = a[0 * 3 + 0];
var a01 = a[0 * 3 + 1];
var a02 = a[0 * 3 + 2];
var a10 = a[1 * 3 + 0];
var a11 = a[1 * 3 + 1];
var a12 = a[1 * 3 + 2];
var a20 = a[2 * 3 + 0];
var a21 = a[2 * 3 + 1];
var a22 = a[2 * 3 + 2];
var b00 = b[0 * 3 + 0];
var b01 = b[0 * 3 + 1];
var b02 = b[0 * 3 + 2];
var b10 = b[1 * 3 + 0];
var b11 = b[1 * 3 + 1];
var b12 = b[1 * 3 + 2];
var b20 = b[2 * 3 + 0];
var b21 = b[2 * 3 + 1];
var b22 = b[2 * 3 + 2];
return [
b00 * a00 + b01 * a10 + b02 * a20,
b00 * a01 + b01 * a11 + b02 * a21,
b00 * a02 + b01 * a12 + b02 * a22,
b10 * a00 + b11 * a10 + b12 * a20,
b10 * a01 + b11 * a11 + b12 * a21,
b10 * a02 + b11 * a12 + b12 * a22,
b20 * a00 + b21 * a10 + b22 * a20,
b20 * a01 + b21 * a11 + b22 * a21,
b20 * a02 + b21 * a12 + b22 * a22,
];
}
}
</script>
</html>주요 수정사항은 다음과 같아요.
- 도형을 삼각형에서 F로 바꾸었어요.
삼각형은 간단한 도형이기 때문에 첫 번째 예제로는 적합하지만 회전했을 때 구분하기 힘들기 때문에 어느 방향에서 봐도 모양이 다른 F를 사용할 거예요. position 배열을 바꿈으로써 수정했지요. - 도형의 색을 검은색으로 바꾸었어요. 가시성을 위해서이지요.
- 평면을 입력시에 0,0 ~ 800,600으로 바꾸고 셰이더에서 clipSpace의 -1,-1 ~ 1,1로 바꾸도록 했어요. 덕분에 해상도가 좋아지죠.
그리고 앞으로 위치를 행렬로 많이 나타낼 거예요. 지금은 2차원만 다루고 있으니 위치는 다음과 같이 행렬로 나타나겠지요.
$\begin{pmatrix}x&y\\\end{pmatrix}$
그리고 간단한 행렬 연산을 소개할게요.
1. 두 행렬을 더하면 각 원소끼리 더해져요.
$\begin{pmatrix}x_1&y_1\\\end{pmatrix}+\begin{pmatrix}x_2&y_2\\\end{pmatrix}=\begin{pmatrix}x_1+x_2&y_1+y_2\\\end{pmatrix}$
2. 행렬에 상수를 곱하면 각 원소에 상수가 곱해져요.
$k\begin{pmatrix}x&y\end{pmatrix}=\begin{pmatrix}kx&ky\\\end{pmatrix}$
3. 두 행렬은 다음과 같이 곱해요.
$\begin{pmatrix}x&y&1\end{pmatrix}\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$
$=\begin{pmatrix}xa_{11}+ya_{21}+a_{31}&xa_{12}+ya_{22}+a_{32}&xa_{13}+ya_{23}+a_{33}\end{pmatrix}$
굉장히 비직관적인 정의이지만 이것 덕분에 우리는 좌표에 변환을 의미하는 행렬을 단지 곱함으로써 변환된 좌표를 얻을 수 있어요!
Translation
도형을 평행 이동하는 건 간단합니다. 도형을 이루는 모든 점을 평행 이동하면 돼요. 이를 위해서 원래 위치 행렬에 각각 값을 더하지요.
$\begin{pmatrix}x&y\\\end{pmatrix}\rightarrow\begin{pmatrix}x+\Delta x&y+\Delta y\\\end{pmatrix}$
Scaling
도형을 scale 하는 것도 쉽습니다. 만약 도형의 어떤 선분이 두 점 A, B를 잇는 선분이라고 할게요.
$\mathrm{A}(x_a,\;y_a)$, $\mathrm{B}(x_b,\;y_b)$
아마 다음과 같이 생겼겠지요. 그리고 이를 X, Y축에 대해 $k$배 scaling 한 결과도 다음과 같습니다.
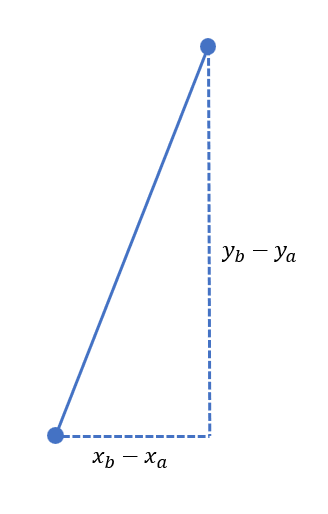

길이가 $k$배가 되도록 맞춘 건데 식을 잘 보면 이는 결국 각 점의 X, Y좌표에 k를 곱한 값임을 알 수 있어요. 따라서 다음과 같이 scaling 할 수 있지요.
따라서 다음과 같이 나타낼 수 있지요.
$\begin{pmatrix}x&y\\\end{pmatrix}\rightarrow\begin{pmatrix}xs_x&ys_y\\\end{pmatrix}$
여기서 $s_x$는 X축 방향의 크기 변화, $s_y$는 Y축 방향의 크기 변화이에요.
조심해야 할 것은 scaling에서 의도치 않게 translation이 발생할 수 있어요. 가령 위의 예시에서는 점 B가 $(x_b,\;y_b)$에서 $(kx_b,\;ky_b)$로 이동하였으니 $((k-1)x_b,\;(k-1)y_b)$만큼 평행 이동했어요. 만약 translation을 없애고 싶으면 이를 상쇄하는 translation을 걸면 돼요. 그러니 다음과 같은 식을 사용할 수 있지요.
$\begin{pmatrix}x&y\\\end{pmatrix}\rightarrow\begin{pmatrix}xs_x-X(s_x-1)&ys_y-Y(s_y-1)\\\end{pmatrix}$
여기서 $X$는 기준점의 x좌표, $Y$는 기준점의 y좌표예요. 도형의 변형은 기준점이 고정된 채 일어나요. 식을 보면 알겠지만 앞선 scale에 의한 translation을 고려하지 않은 식은 $X=Y=0$인 특수한 경우, 즉 scaling의 기준점이 원점인 경우이지요.
Rotation
Rotation은 머리를 좀 써야 해요. 삼각함수가 사용되거든요.
우선 회전에는 기준점이 필요해요. 회전의 중심이 되는 점이지요. 원점이라고 가정하고 진행할게요. 그럼 좌표평면 위 임의의 점에 대해 다음과 같이 쓸 수 있어요.

그림에는 $r=1$인 단위원이 그려져 있지만 임의의 반지름을 가진 원에 대해 증명하고자 해요. 점 $P$를 시계 반대방향으로 $b$만큼 회전한 점이 $P^{\prime}$이에요.
이때 삼각함수의 덧셈 정리를 사용하면 $P^{\prime}$의 좌표는 다음과 같지요.
$P^\prime\left(r(\cos{a}\cos{b}-\sin{a}\sin{b}),\;r(\sin{a}\cos{b}+\cos{a}\sin{b}) \right)$
그런데 $P(r\cos(a),\;r\sin{a})=P(x,\;y)$로 잡으면 문자들을 치환해서
$P^\prime\left(x\cos{b}-y\sin{b},\;y\cos{b}+x\sin{b}) \right)$
따라서 원점을 축으로 하는 회전은 다음과 같이 표현되지요.
$\begin{pmatrix}x&y\\\end{pmatrix}\rightarrow\begin{pmatrix}x\cos{\theta}-y\sin{\theta}&x\sin{\theta}+y\cos{\theta}\\\end{pmatrix}$
여기서 $\theta$는 회전하는 각으로 시계 반대 방향이 양의 부호를 가져요. 만약 시계방향이 양의 부호를 가지게 하고 싶다면 $P^\prime\left(r\cos{a-b},\;r\sin{a-b} \right)$ 로 두고 같은 방식으로 유도하면 다음과 같이 나와요.
$\begin{pmatrix}x&y\\\end{pmatrix}\rightarrow\begin{pmatrix}x\cos{\theta}+y\sin{\theta}&-x\sin{\theta}+y\cos{\theta}\\\end{pmatrix}$
만약 축이 원점이 아닌 임의의 점 $O(X,\;Y)$라면 어떻게 될까요?

$P$와 $P^\prime$은 원점이 기준점일 때와 절대적인 좌표는 바뀌지 않았어요. 하지만 원의 중심이 이동했기 때문에 이들의 좌표는 다음과 같이 같이 평행 이동되어야 하지요.
$P(r\cos{a}+X,r\sin{a}+Y)$
$P^\prime(r\cos{(a+b)}+X,r\sin{(a+b)}+Y)$
위에서 했던 대로 $P^\prime$의 삼각함수를 덧셈 정리로 전개하면
$P^\prime\left(r(\cos{a}\cos{b}-\sin{a}\sin{b})+X,\;r(\sin{a}\cos{b}+\cos{a}\sin{b})+Y \right)$
원래 $P$의 좌표가 $P(x,y)$라고 가정하면 다음과 같은 식이 성립하므로
$x=r\cos{a}+X$, $r\cos{a}=x-X$
$y=r\sin{a}+Y$, $r\sin{a}=y-Y$
$P^\prime$에 대입하면
$P^\prime\left((x-X)\cos{b}-(y-Y)\sin{b}+X,\;(y-Y)\cos{b}+(x-X)\sin{b}+Y \right)$
미지수와 상수를 분리해서 표현하면
$P^\prime\left(x\cos{b}-y\sin{b}-X(\cos{b}-1)+Y\sin{b},\;x\sin{b}+y\cos{b}-X\sin{b}-Y(\cos{b}-1)\right)$
즉 다음과 같이 변환하는 거에요.
$\begin{pmatrix}x&y\\\end{pmatrix}$$\rightarrow\begin{pmatrix}x\cos{\theta}-y\sin{\theta}-X(\cos{\theta}-1)+Y\sin{\theta}&x\sin{\theta}+y\cos{\theta}-X\sin{\theta}-Y(\cos{\theta}-1\\\end{pmatrix}$
Scaling과 같이 앞선 축이 원점인 경우는 $X=Y=0$인 특수한 경우임을 확인할 수 있지요.
행렬로 변환 처리하기
이상의 방법으로 우리는 임의의 점에 대해 3가지 변환을 수행할 수 있지만 이들을 각각 다루면서 변환에 변수들을 할당해서 컨트롤하는 것은 매우 복잡해요. 그래서 행렬을 통해 각 변환을 하나로 묶어서 관리할 겁니다.
앞서서
$\begin{pmatrix}x&y&1\end{pmatrix}\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$
$=\begin{pmatrix}xa_{11}+ya_{21}+a_{31}&xa_{12}+ya_{22}+a_{32}&xa_{13}+ya_{23}+a_{33}\end{pmatrix}$
라고 했어요. 따라서 이것의 계산 결과가 되는 행렬이 다시 x, y, z 행렬로 나온다면 새로운 행렬의 원소, 가령 새로운 x 값은 다음과 같이 계산됩니다. 이걸 따라가며 다음 설명을 잘 읽어봐요.
| $\mathrm{newX}=$ | $xa_{11}+$ |
| $ya_{21}+$ | |
| $a_{31}+$ |
Translation
이걸 보면 $a_{11}$이나 $a_{21}$에 상관없이 $a_{31}$에 $\Delta x$를 넣으면 기존 점에 더해져서 평형 이동이 되겠네요. 따라서 행렬의 $a_{3n}$들의 값은 정해져요. 그러니 translation 행렬은 다음과 같으면 되지요.
$\begin{pmatrix}1&0&0\\0&1&0\\\Delta x&\Delta y&1\end{pmatrix}$
Scaling
앞서서 기준점이 원점인 경우, 기준점이 임의의 점인 경우에 대해 설명했어요. 이것도 각각 행렬로 나타낼 수 있지요. 기준점이 $(X,\;Y)$인 경우 scaling 행렬은 다음과 같아요.
$\begin{pmatrix}s_x&0&0\\0&s_y&0\\-X(s_x−1)&-Y(s_y−1)&1\end{pmatrix}$
특히 기준점이 원점인 경우 scaling 행렬은
$\begin{pmatrix}s_x&0&0\\0&s_y&0\\0&0&1\end{pmatrix}$
이지요.
Rotation
앞선 논의를 행렬로 옮겨서 표현하면 rotation 행렬은 다음과 같아요. 만약 축이 $(X,Y)$이고 시계 반대방향을 양의 방향으로 정하면 rotation 행렬은
$\begin{pmatrix}\cos{\theta}&\sin{\theta}&0\\-\sin{\theta}&\cos{\theta}&0\\-X(\cos{\theta}-1)+Y\sin{\theta}&-X\sin{\theta}-Y(\cos{\theta}-1)&1\end{pmatrix}$
특히 기준점이 원점이라면
$\begin{pmatrix}\cos{\theta}&\sin{\theta}&0\\-\sin{\theta}&\cos{\theta}&0\\0&0&1\end{pmatrix}$
이지요.
이제 3개의 변환에 대해 각각의 변환에 사용되는 행렬을 구했어요. 이 행렬을 점의 좌표를 의미하는 행렬에 곱하면 변환된 점이 나오지요. 그런데 생각해보면 원래 점 $P$에 translation 행렬을 곱해서 $P^{\prime}$을 얻고, scaling 행렬을 곱해서 $P^{\prime\prime}$을 얻고, rotation 행렬을 곱해서 $P^{\prime\prime\prime}$을 차례로 얻는 대신 행렬곱에 대한 다음 성질을 사용할 수 있어요.
세 행렬 $A$, $B$, $C$에 대해
$ABC=A(BC)=(AB)C$ ... 행렬곱의 결합 법칙
따라서 변환할 점을 $P$, translation 행렬을 $T$, scaling 행렬을 $S$, rotation 행렬을 $R$이라고 한다면 $PTSR$을 계산하는 대신 $X=TSR$로 두고 $P^\prime=PX$로 하는 편이 간단해요.
한편 행렬을 구성하면서 왜 3행 3열의 값이 0이 아닌 1인지 의문을 가질 수 있어요. 바로 변환에 사용되는 행렬들을 서로 곱할 때 translation 정보가 사라지는 것을 막기 위해서예요. 직접 계산해보면 왜 여기가 0이 아닌 1이어야 하는지 알 수 있지요. 예를 들어 translation 행렬($T$)과 다른 변환에 사용되는 행렬 ($M$)이 있다고 해요.
$T=\begin{pmatrix}0&0&0\\0&0&0\\200&100&1\\\end{pmatrix}$
$M=\begin{pmatrix}1&0&0\\0&2&0\\0&0&1\\\end{pmatrix}$
이 둘을 곱하게 되면($MT$) 다른 부분은 무시하고 row 3만 보면 translation에 대한 정보가 살아있어야 하기 때문에 우리가 기대하는 결과는 이거예요.
$\begin{pmatrix}200&100&1\\\end{pmatrix}$
그리고 위와 같이 3행 3열이 1인 경우에는 이 값이 제대로 나오지요. 하지만 0인 경우에는 0이 translation 값과 곱해져서 0으로 날아가요. 그래서 여기는 1이어야 해요.
또 중요한 건 행렬끼리의 곱은 교환 법칙이 성립하지 않는다는 점이에요. 그러니 세 변환을 적용하는 순서에 따라 결과물이 달라질 수 있어요. 예를 들어 똑같은 변형을 가해도 다음과 같이 전혀 다른 결과물을 얻을 수 있어요. 이것에 대한 판단은 먼저 적용한 변형이 좌표평면 전체를 변형한다고 생각하면 돼요.

이건 변형이 없는 상태예요.
여기에 (200, 100)만큼 translation을 하고 (2, 1)만큼 scaling을 해서 (800, 600)의 캔버스 위에 그리면 다음과 같이 다른 2개의 결과물을 얻을 수 있어요.


왼쪽 사진에서는 먼저 적용된 scaling의 결과로 좌표 전체가 마치 고무줄처럼 2배로 늘어났어요. 그래서 보이는 좌표 영역은(800, 600)에서 (400, 600)으로 바뀌었어요. 그 상태에서 F가 200만큼 x축으로 움직였으니 중간 정도로 F가 왔죠.
하지만 translation을 먼저 진행하면 원점(F의 왼쪽 맨 위에 있음)이 함께 움직이기 때문에 나중에 오는 scaling에는 영향이 없죠.
translation와 rotation의 적용 순서는 더 재밌는 결과를 만들어요. 다음은 $\frac{\pi}{4}$만큼 회전과 평행이동을 적용한 결과에요.


왼쪽 이미지는 translation을 먼저 적용했기 때문에 rotation을 적용할 때 F를 따라 같이 이동한 원점을 축으로 회전했어요.
그런데 rotation을 먼저 적용하니 F가 대각선으로 움직였어요. 이는 rotation이 좌표평면을 통째로 회전시켰기 때문이에요. 그래서 분명 좌표평면의 각 축에 평행하게 움직였지만 밖에서 보기에는 대각선으로 움직인 것처럼 보이는 것이죠.
그런데 눈치가 빠른 분은 이상한 점을 알아챘을 거예요. 저는 분명 앞에서 반시계 방향이 양의 부호를 갖는 식을 유도해서 적용했어요. 그런데 $\frac{\pi}{4}$, 즉 45도만큼 회전한 결과가 시계방향으로 돌아가 있어요! 이 오류가 발생한 이유는 뒤에서 설명할게요. 일단은 넘어가죠.
WebGL에 응용하기
이상의 논의를 WebGL에 응용해서 맨 처음에 만든 F를 변환하여보죠.
우선 각 변환에 대한 행렬을 만들어주는 javascript 코드를 작성해요.
/**
* 평행 이동 행렬을 만듭니다.
* @param{number} dx x축 평형 이동
* @param{number} dy y축 평행 이동
* @return{Array.number} 평행 이동 행렬
*/
function translation(dx, dy) {
return [
1, 0, 0,
0, 1, 0,
dx, dy, 0
];
}
/**
* 크기 조정 행렬을 만듭니다.
* @param{number} sx x축 크기 배율
* @param{number} sy y축 크기 배율
* @return{Array.number} 크기 조정 행렬
*/
function scale(sx, sy) {
return [
sx, 0, 0,
0, sy, 0,
0, 0, 0
]
}
/**
* 기준점을 가진 크기 조정 행렬을 만듭니다.
* @param{number} sx x축 크기 배율
* @param{number} sy y축 크기 배율
* @param{number} originX 기준점의 x 좌표
* @param{number} originY 기준점의 y 좌표
* @return{Array.number} 크기 조정 행렬
*/
function scale(sx, sy, originX, originY) {
return [
sx, 0, 0,
0, sy, 0,
-originX*(sx-1), -originY(sy-1), 0
]
}
/**
* 회전 변환 행렬을 만듭니다.
* @param{number} angle 시계방향을 +로 하는 회전 각도(radian)
* @return{Array.number} 회전 변환 행렬
*/
function rotation(angle) {
const s = Math.sin(angle), c = Math.cos(angle);
return [
c, s, 0,
-s, c, 0,
0, 0, 0
];
}
/**
* 축을 가진회전 변환 행렬을 만듭니다.
* @param{number} angle 시계방향을 +로 하는 회전 각도(radian)
* @param{number} originX 기준점의 x 좌표
* @param{number} originY 기준점의 y 좌표
* @return{Array.number} 회전 변환 행렬
*/
function rotation(angle, originX, originY) {
const s = Math.sin(angle), c = Math.cos(angle);
return [
c, s, 0,
-s, c, 0,
-originX*(c-1)+originY*s, -originX*s-originY*(c-1), 0
]
}그리고 세 변환에 대한 행렬을 곱하여 최종적인 하나의 변환 행렬을 만들려면 3x3 행렬 두 개를 곱하는 함수도 만들어야죠.
var m3 = {
multiply: function(a, b) {
var a00 = a[0 * 3 + 0];
var a01 = a[0 * 3 + 1];
var a02 = a[0 * 3 + 2];
var a10 = a[1 * 3 + 0];
var a11 = a[1 * 3 + 1];
var a12 = a[1 * 3 + 2];
var a20 = a[2 * 3 + 0];
var a21 = a[2 * 3 + 1];
var a22 = a[2 * 3 + 2];
var b00 = b[0 * 3 + 0];
var b01 = b[0 * 3 + 1];
var b02 = b[0 * 3 + 2];
var b10 = b[1 * 3 + 0];
var b11 = b[1 * 3 + 1];
var b12 = b[1 * 3 + 2];
var b20 = b[2 * 3 + 0];
var b21 = b[2 * 3 + 1];
var b22 = b[2 * 3 + 2];
return [
b00 * a00 + b01 * a10 + b02 * a20,
b00 * a01 + b01 * a11 + b02 * a21,
b00 * a02 + b01 * a12 + b02 * a22,
b10 * a00 + b11 * a10 + b12 * a20,
b10 * a01 + b11 * a11 + b12 * a21,
b10 * a02 + b11 * a12 + b12 * a22,
b20 * a00 + b21 * a10 + b22 * a20,
b20 * a01 + b21 * a11 + b22 * a21,
b20 * a02 + b21 * a12 + b22 * a22,
];
}
}
vertex shader가 tranform 행렬을 위치 행렬에 곱해서 반환하도록 업데이트해요.
attribute vec2 a_position;
uniform vec2 u_resolution;
uniform mat3 transform;
void main() {
vec2 position = (transform * vec3(a_position, 1)).xy;
vec2 clipSpace = ((position / u_resolution) * 2.0)-1.0;
gl_Position = vec4(clipSpace * vec2(1, -1), 0, 1);
}전편과는 달리 셰이더에 뭐가 많아졌어요.
우선 transform은 변환 행렬이에요. a_position에 transform을 곱해서 원하는 변형이 이루어진 행렬을 얻을 수 있지요.
그 뒤로는 clipSpace로 평면을 변형하는 것이에요. 그 과정은 다음과 같지요.

이때 평면을 위아래로 대칭하는 작업이 있어요. 이 때문에 일부 작업이 의도대로 보이지 않을 수 있어요. 예를 들어서 회전이죠. 앞서서 저는 반시계 방향이 양의 부호를 가지는 식을 유도해서 사용했어요. 그런데 회전 방향의 예상과는 반대였죠. 그 이유가 평면을 위아래로 뒤집었기 때문에 회전 방향이 반대가 된 것이에요.
이 외의 내용은 모두 이미 앞에서 다룬 내용이니 빠르게 넘어갈게요.
var resolutionLocation = gl.getUniformLocation(program, "u_resolution");
const transformUniformLocation = gl.getUniformLocation(program, "transform");resolution uniform과 transform uniform 위치 찾기(초기화 코드)
const translateMatrix = transform.translate(dx, dy);
const scaleMatrix = transform.scale(sx, sy);
const rotateMatrix = transform.rotate(angle);
const transformMatrix = m3.multiply(m3.multiply(translateMatrix, rotateMatrix), scaleMatrix);
gl.uniformMatrix3fv(transformUniformLocation, false, transformMatrix);각 변환 행렬을 얻어오기 > 각 변환 행렬을 곱해서 하나의 변환 행렬 만들기 > uniform에 변환 행렬 넣기
var dx=200, dy=100, sx=1, sy=1, angle=0;
const pi = Math.PI;변환 정도를 가진 변수와 원주율을 가진 상수 만들기
