현실의 많은 것은 양의 상관관계를 가지고 있다. 가령 공부를 많이 하면 시험 점수가 올라가고, 밥을 많이 먹을수록 몸무게가 증가한다. 이러한 것들을 분석하기 위한 모델이 선형 회귀(Linear Regression)이다.
선형회귀분석은 데이터의 입력(X)과 출력(Y)이 선형적인 관계를 가질 것으로 예측한다. 가령 하나의 입력을 받아 하나의 출력을 만드는 데이터는 다음과 같은 관계를 생각할 수 있다.
$Y=WX+b$
일차함수 모양이다. 우리는 이러한 관계를 Hypothesis(가설)이라고 하여 함수 $H(X)$로 표현한다. 즉, 하나의 입력이 있는 선형 회귀의 Hypothesis는 다음과 같다.
$H(X)=WX+b$
여기서 $X$는 입력 데이터, $W$는 웨이트(weight), $b$는 바이어스(bias)이다. $X$와 $Y$의 순서쌍들은 학습용 데이터셋으로 주어져 있다. 우리가 해야 할 것은 데이터셋으로부터 데이터에 가장 잘 맞는 $W$와 $b$의 값을 알아내는 것이다.
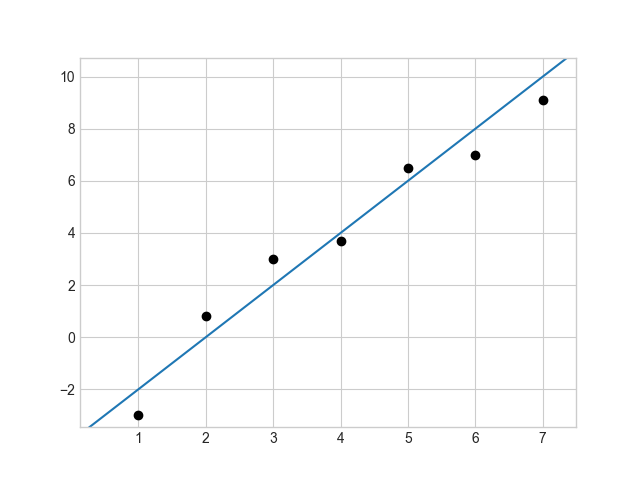
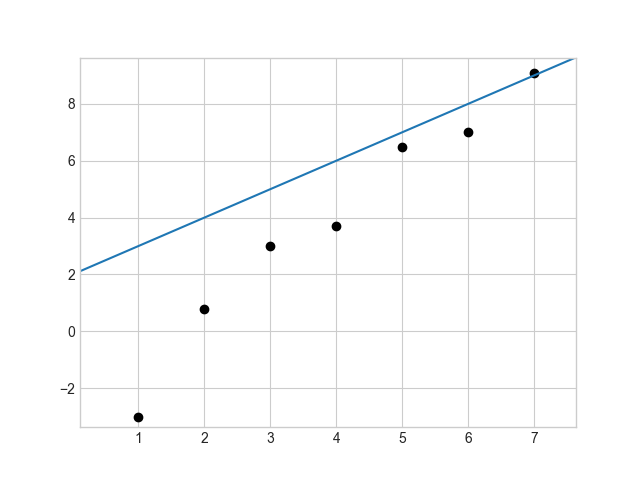
위 그림은 앞선 Hypothesis에 $W$와 $b$값을 임의로 설정하여 만든 두 개의 모델이다. 검은색 점은 데이터이고, 파란색 직선이 예측한 모델이다. 왼쪽과 오른쪽 중 무엇이 데이터에 더 잘 맞을까? 당연히 왼쪽 모델이다. 하지만 컴퓨터는 이를 인간처럼 직관적으로 파악할 수 없다. 따라서 어떤 모델이 데이터에 얼마나 잘 맞는지 계산해주는 cost 함수(loss 함수)를 만들어야 한다.
일반적으로 입력 $X$에 대해 예측($H(X)$)과 실제 데이터($Y$)의 차이는 다음과 같이 구한다.
$H(X)-Y$
그런데 이 값은 양수일 수도, 음수일 수도 있기 때문에 여기에 제곱을 한다. 제곱을 함으로써 부호도 맞춰주지만 멀리 떨어진 점에 대해 가까운 점에 비해 더 큰 페널티를 부여할 수 있다.
$\left(H(X)-Y\right)^2$
이제 모든 $m$개의 데이터에 대해 예측과 실제 데이터의 차이의 제곱을 평균내는 식을 구성하면 다음과 같다.
$\frac{1}{m}\displaystyle\sum_{n=1}^{m}{\left(H(X_n)-Y_n\right)^2}$
이 함수를 cost 함수라 하여 다음과 같이 쓴다.
$cost=\frac{1}{m}\displaystyle\sum_{n=1}^{m}{\left(H(X_n)-Y_n\right)^2}$
그런데 함수 $H(X)$는 $W$와 $b$의 함수이므로 cost 함수 또한 $W$와 $b$의 함수로 작성하여 다음과 같이 쓸 수 있다.
$cost(W,\;b)=\frac{1}{m}\displaystyle\sum_{n=1}^{m}{\left(H(X_n)-Y_n\right)^2}$
cost 함수의 값을 최소로 만드는 $W$와 $b$의 값을 알아낸다면 그것으로 다른 데이터들도 예측할 수 있는 모델을 만들 수 있다. cost 함수의 값을 최소로 하는 변수들의 값을 찾아내는 과정이 흔히 말하는 "학습"과정이다.
이 상황에서는 cost 함수의 값을 최소로 만드는 변수들의 값을 찾아내기 위해 경사 하강법(Gradient descent)을 사용할 것이다.
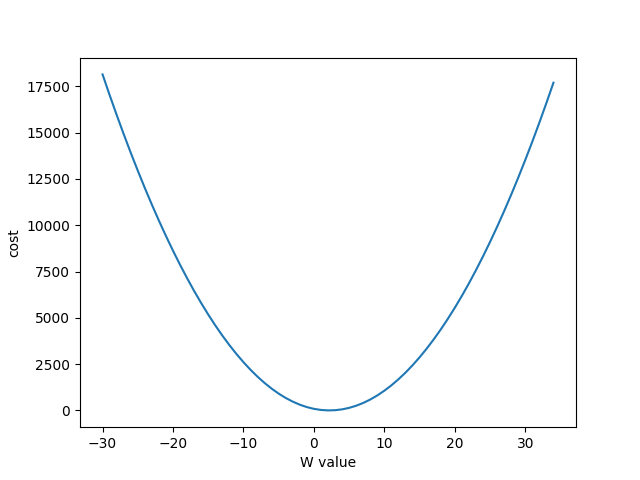
위 그래프는 일단 편의를 위해 Hypothesis에서 $b$항을 제거한 후 $W$의 값을 -30에서 +35까지 늘려가며 cost의 값을 계산한 결과이다. 여기서 사용한 데이터는 다음과 같다.
| $X$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| $Y$ | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
이차함수의 그래프와 비슷하게 생겼다.
이 함수의 최소는 대략 2쯤에 있어 보인다. 하지만 역시 컴퓨터는 이를 직관적으로 알 수 없다. 그래서 W의 값을 최적화하는 방법을 구성해야 한다.
W값을 최적화하기 위해 일단 $W$의 값을 임의의 값으로 설정하고 시작한다. 가령 W=20에서 시작하면 다음과 같은 모습일 것이다.
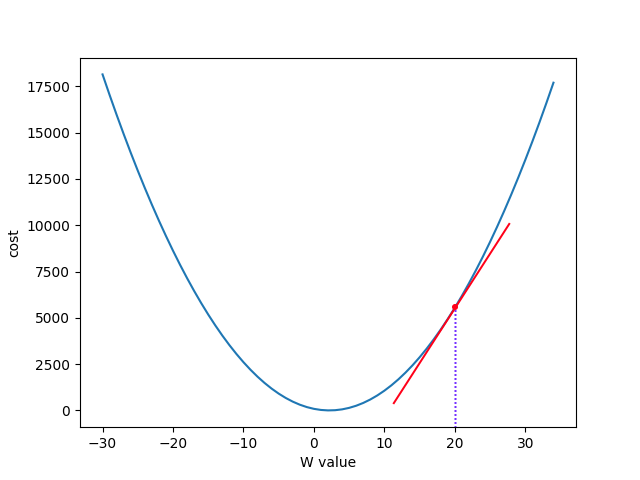
여기서 빨간색 선은 그래프의 접선이다. 접선의 기울기가 양수인데 이는 곧 최저점이 왼쪽에 있음을 말한다. 따라서 $W$ 값을 줄여야 한다. 마찬가지로 접선의 기울기가 음수라면 최저점이 오른쪽에 있다는 뜻이니 $W$ 값을 늘려야 한다. 이 상황은 다음과 같은 식으로 나타낼 수 있다.
$W := W-\alpha\frac{\partial}{\partial W}cost(W)$
여기서 $\alpha$는 Learning rate이다. $\frac{\partial}{\partial W}cost(W)$는 cost 함수를 $W$에 대해 미분한 값이니 여기에 $\alpha$를 곱하면 기울기가 클 수록, 또는 Learning rate가 클 수록 $W$의 값을 많이많이 변화시키면서 학습시킬 수 있다.
$\frac{\partial}{\partial W}cost(W)$
여기에 $cost(W)$를 대입하면 다음과 같다.
$\frac{\partial}{\partial W}{\frac{1}{m}\displaystyle\sum_{n=1}^{m}{\left(WX_n-Y_n\right)^2}}$
미분하면 다음과 같다.
$\frac{1}{m}\displaystyle\sum_{n=1}^{m}{2\left(WX_n-Y_n\right)X_n}$
cost 함수에서 각 값 들이 2배가 되던 1/2배가 되던 중요한 것은 아니니 시그마에서 2를 없애줘서 쓰면 다음과 같다.
$\frac{1}{m}\displaystyle\sum_{n=1}^{m}{\left(WX_n-Y_n\right)X_n}$
이를 앞선 경사 하강법의 식에 대입하면 다음이 된다.
$W := W-\alpha\frac{1}{m}\displaystyle\sum_{n=1}^{m}{\left(WX_n-Y_n\right)X_n}$
그런데 경사 하강법을 항상 쓸 수 있는 것은 아니다. 예를 들어 cost 함수가 다음과 같이 생겼다면
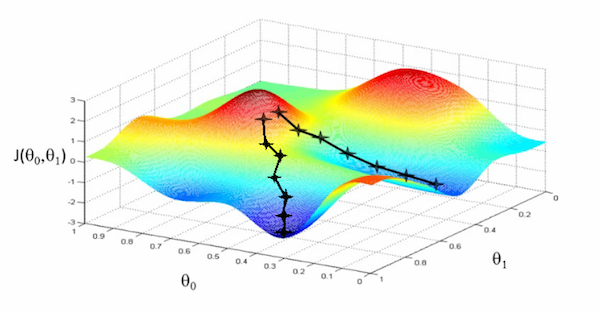
어떤 점에서 갈 수 있는 최저점은 2개가 있다. 이런 경우에는 단순한 경사하강법을 쓰기는 힘들다. 이번 경우에는 cost 함수가 다음과 같이 볼록(convex) 하기 때문에 경사 하강법이 적합하다.
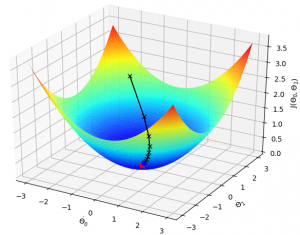
이것을 가지고 인공지능을 직접 만들어보자.
Python을 사용하여 Tensorflow 2 기반으로 코드를 작성할 것이다.
import numpy as np
import tensorflow as tf
x_train = [1, 2, 3, 4, 5]
y_train = [-3, -1, 1, 3, 5]
tf.model = tf.keras.Sequential()
# units = 출력 텐서 shape, input_dim = 입력 텐서 shape
tf.model.add(tf.keras.layers.Dense(units=1, input_dim=1))
sgd = tf.keras.optimizers.SGD(lr=0.0426) # lr = learning rate
tf.model.compile(loss='mse', optimizer=sgd) # mse =mean_squared_error
tf.model.summary()
# fit 함수는 학습을 실행합니다.
tf.model.fit(x_train, y_train, epochs=300)
# predict 함수는 주어진 값을 모델을 통해 예측합니다
y_predict = tf.model.predict(np.array([7, 10]))
print(y_predict)
for layer in tf.model.layers: print("W=", layer.get_weights()[0], ", b=", layer.get_weights()[1])학습해보면 최종적인 cost는 9.6283e-4 가 나오고 각 변수들의 값은 다음과 같이 정해졌다.
$W=1.9801447$, $b=-4.9283166$
그러니 모델은 다음과 같이 나온 것이다.
$Y=1.9801447X-4.9283166$
실제 함수가 $Y=2X-5$임을 생각하면 매우 잘 학습한 모습이다.
학습된 모델에 [7, 10]을 입력해보면 [[ 8.932697], [14.873131]] 가 결과로 나온다. $X=7$인 경우 $Y=8.9$ 정도 하고, $X=10$인 경우 $Y=14.9$ 정도 나온다는 의미이다. 이 또한 원래 함수와 비교해봤을 때 매우 비슷함을 알 수 있다.
한편 선형 회귀에서 반드시 입력이 하나일 필요는 없다. 다음 데이터를 생각해보자.
| 중간 | 기말 | 중간 | 기말(예측할 값) |
| 96 | 95 | 100 | 97 |
| 56 | 50 | 30 | 45 |
| 71 | 69 | 88 | 85 |
| 49 | 53 | 60 | 57 |
| 23 | 27 | 30 | 28 |
이를 바탕으로 두 번의 중간고사와 한 번의 기말고사 성적을 가지고 마지막 기말고사 성적을 예측하는 인공지능을 만들어보자. 일반적으로 한 과목에서 다른 시험을 잘 볼수록 남은 시험도 잘 볼 가능성이 높아지니 여기서 X와 Y는 양의 상관관계를 가지고 있다.
여기서 Hypothesis는 다음과 같다(물론 $b$항은 생략 한 상태이다).
$H(x_1,\;x_2,\;x_3)=w_1x_1+w_2x_2+w_3x_3$
그런데 텐서에서 스칼라곱을 생각해보면 위 Hypothesis는 다음과 같이 두 텐서의 곱으로 나타낼 수 있다.
$H(x_1,\;x_2,\;x_3)$$=\begin{pmatrix}x_1&x_2&x_3\end{pmatrix} \cdot \begin{pmatrix}w_1\\w_2\\w_3\end{pmatrix}$$=x_1w_1+x_2w_2+x_3w_3$
그래서 다음과 같이 치환하면
$X=\begin{pmatrix}x_1&x_2&x_3\end{pmatrix}$, $W=\begin{pmatrix}w_1\\w_2\\w_3\end{pmatrix}$
Hypothesis를 다음과 같이 간단하게 쓸 수 있다.
$H(X)=X \cdot W$
만약 각각의 데이터에 대한 $H(X)$의 값을 한 번에 계산하려면 다음과 같이 텐서를 구성하고
$X=\begin{pmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{pmatrix}$, $W=\begin{pmatrix}w_1\\w_2\\w_3\end{pmatrix}$
$X\cdot W$
를 계산하게 되면 다음과 같은 텐서가 나오게 된다.
$\begin{pmatrix}x_{11}w_1+x_{12}w_2+x_{13}w_3\\x_{21}w_1+x_{22}w_2+x_{23}w_3\\x_{31}w_1+x_{32}w_2+x_{33}w_3\end{pmatrix}$
각 열마다 $H(X)$의 값이 잘 들어간 걸 확인할 수 있다.
이렇게 가설만 설정해주면 앞선 방식과 같게 cost가 최소가 되는 weight를 계산해서 결과를 낼 수 있다.
입력이 여러 개인 선형 회귀를 multi-variable linear regression이라고 한다. 이것을 Tensorflow 2에서 구현하면 다음과 같다.
import numpy as np
import tensorflow as tf
x_train = tf.constant([
[96, 95, 100],
[56, 50, 30],
[71, 69, 88],
[49, 53, 60],
[23, 27, 30]
])
y_train = tf.constant([
[97],
[45],
[85],
[57],
[28]
])
tf.model = tf.keras.Sequential()
tf.model.add(tf.keras.layers.Dense(units=1, input_dim=3))
sgd = tf.keras.optimizers.SGD(lr=0.00007)
tf.model.compile(loss='mse', optimizer=sgd)
tf.model.fit(x_train, y_train, epochs=30000)
for layer in tf.model.layers: print("W=", layer.get_weights()[0], ", b=", layer.get_weights()[1])
y_predict = tf.model.predict(np.array([[96, 96, 96], [96, 96, 100], [83, 100, 100], [97, 96, 97], [92, 96, 100]]))
print(y_predict)실행시켜보면 다음과 같이 결과가 나온다.
$W=\begin{pmatrix}0.78409445\\-0.4193496\\0.6210407\end{pmatrix}$, $b=2.139845$
cost = 2.6475
첫 번째 기말에서 weight가 음수를 가지고 있다, 이말인 곧 첫번째 기말을 잘 볼수록 두 번째 기말을 못 본다는 말이다.
조금 의아하긴 하지만 한번 예측해보자.
| 중간 | 기말 | 중간 | 기말(인공지능 예측) | 기말(실제 점수) |
| 96 | 96 | 96 | 96.77525780 | 94 |
| 96 | 96 | 100 | 99.25942060 | 95 |
| 83 | 100 | 100 | 87.38879435 | 96 |
| 97 | 96 | 97 | 98.18039295 | 100 |
| 92 | 96 | 100 | 96.12304280 | 96 |
학습에 사용한 데이터가 실제 데이터를 기반으로 하지 않은 점을 고려하면 그럭저럭 예측에 성공한 모습이다. 예측한 점수와 실제 점수의 차이가 한 과목을 제외하면(이 과목은 중간에 재미가 붙었다) 일반적으로 4점 아래이다.
'이것저것 > AI' 카테고리의 다른 글
| Softmax Regression Classification (0) | 2022.03.09 |
|---|---|
| 로지스틱 회귀를 사용한 분류(Logistic regression classification) (0) | 2022.01.16 |
| 인공지능 - 머신러닝의 개념 (0) | 2021.12.28 |
