알림: 이 글은 경로의 개수 Pt. 1의 심화 내용입니다. 앞선 글을 이해하지 못한 상태로 이 글을 읽으시면 많이 어려우실 수 있습니다.
우리는 앞서 격자모양의 지도에서 최단거리를 구하는 방법을 탐구하였다. 이번에서도 특별한 경우에서 최단경로를 구해보자.
들어가기
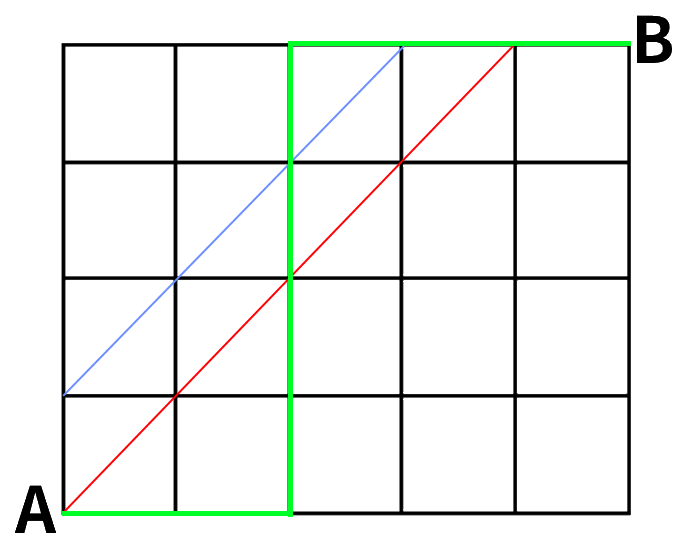
먼저 이번 글에서 내내 다루게 될 한 개의 문제를 소개하겠다.

문제:
왼쪽과 같은 지도가 있다. A에서 B까지의 최단경로 중
- 푸른색 선분 위의 점을 통과하지 않는 경로의 개수를 구하여라
- A점을 제외한 붉은색 선분 위의 점을 통과하지 않는 경로의 개수를 구하여라.
이번 글에서는 위의 문제만 다룰 것이다. 문제의 조건과 상황을 잘 이해하자. 예를 들면 1번의 경우 Fig1-1a와 같은 경로는 되는 경로이며 Fig1-1b와 같은 경로는 되지 않는 경우이다.

우선 아래 설명은 1번 문제를 집중적으로 다루겠다.
여사건으로 접근하기
우리가 구하고자 하는 경우의 수는 (A-B의 전체 최단경로의 개수)-(파란색 선분 위의 점을 지나는 최단경로의 개수)로 구할 수 있을 것이다. 전체 최단경로의 개수는 쉽게 구할 수 있으니, 파란색 선분 위의 점을 지나는 최단경로의 개수만 구하면 문제가 해결될 것이다.
이제 문제가 최단경로 중에서 파란색 선분 위의 점을 지나는 경로의 수를 구하는 문제로 바뀌었다. 이제 어떤 최단경로들이 반드시 파란색 선분을 넘게 되는지 생각해보자.
반사의 원리 사용하기

Fig3-1은 점 A를 푸른색 선에 대칭시키어 A'을 만들고 새 점의 위치에 맞도록 지도를 조금 확장한 모습이다.
우리가 이렇게 대칭을 시킨 이유를 결론부터 말하자면 A에서 B까지 파란선 위의 점을 지나서 가는 경로의 수를 대응을 통해 구하기 위해서이다. 자세히 말하자면, A에서 B까지 파란선 위의 점을 지나서 이동하는 경로의 수는 A'에서 B까지의 최단경로의 수와 같다.
우선 A'에서 B까지 이동하는 모든 경로는 파란선을 통과할 수밖에 없음을 확인하자. 별도의 설명 없이 직관적으로 이해가 된다.


Fig3-2는 A'에서 B까지의 최단경로 중 한 개를 나타낸 것이다. 파란선을 지나며 B까지 이동하고 있음을 알 수 있다.
이제 A'부터 녹색 경로가 파란선에 닿는 점 사이의 구간을 파란색 선분으로 대칭시켜보자. 이제 뭔가가 보일 것이다.
A'에서 B까지 이동하는 경로가 A에서 B까지 파란선을 거쳐서 이동하는 경로로 바뀌었다. 앞에서 우리는 A'에서 B까지의 모든 경로가 파란선을 지나기 때문에 모든 경로에 대해서 앞서 한 것과 같이 대칭을 시켜주면 A에서 B까지 파란선을 거쳐 이동하는 경로가 된다. 즉, 경우가 모두 대응되는 것이다.
따라서 A에서 B까지 파란선을 거쳐서 이동하는 최단경로의 수는 A'에서 B까지 파란선을 거쳐 이동하는 최단경로의 수와 같다. 즉, $\frac{9!}{6!3!}=84$가지이다.
이제 앞서 알아본 여사건을 이용해 답을 구하면 (A-B의 전체 최단경로의 개수)-(파란색 선분 위의 점을 지나는 최단경로의 개수)=$\frac{9!}{5!4!}-\frac{9!}{6!3!}$$=126-84$$=42$가지이다.
일반화하기
일반적으로, $(0,0)$에서 $(n,m)$까지 $y=x+1$ 위의 점을 지나지 않으며 정수점만을 통과하여 이동하는 최단경로의 개수는 다음과 같다. (참고로, 이 상황은 우리가 앞서 알아본 상황에서 $(5,4)$를 $(n,m)$으로 바꾼 게 전부이다.)
$\frac{(n+m)!}{n!m!}-\frac{(n+m)!}{(n+1)!(m-1)!}$
조금만 생각하면 위의 일반화된 식도 앞서 구한 풀이과정 중 나온 식과 크게 다름이 없음을 알 수 있다.
한편, 위의 경우중 특수한 경우를 따로 구분하기도 한다. $(0,0)$에서 $(n,n)$까지 $y=x+1$위의 점을 지나지 않으며 정수점만을 통과하여 이동하는 최단경로의 개수는 다음과 같다.
$\frac{1}{n+1}({}_{2n}\mathrm{C}_n$)
사실 위 식도 앞서 구한 일반적인 식의 변형에 불과한다. 위 식은 다음과 같이 유도한다.
$(0,0)$에서 $(n,n)$까지 $y=x+1$위의 점을 지나지 않고, 정수점만을 지나는 최단경로의 개수는 앞서 일반화한 내용에 따라 $\frac{(2n)!}{n!n!}-\frac{(2n!)}{(n+1)!(n-1)!}$이다.
분수를 합치기 위해 $n!n!$으로 통분을 하면 다음과 같은 식이 된다: $\frac{(2n)!}{n!n!}-\frac{\frac{(2n)!n}{n+1}}{n!n!}$
분모가 같아졌으니 공통 인수로 묶어주고 분수를 합칠 수 있다: $\frac{(2n)!}{n!n!}(1-(\frac{n}{n+1}))
$$=\frac{(2n)!}{n!n!}\frac{1}{n+1}$
한편 $\frac{2!}{n!n!}$$={}_{2n}\mathrm{C}_n$이므로 앞서 구한 식에 대입해주면 경우의 수는 ${}_{2n}\mathrm{C}_n \times \frac{1}{n+1}$임을 구할 수 있다.
우리는 이런 특수한 케이스에서의 경우의 수를 카탈란 수라고 한다. 카탈란 수는 $n$이 음이 아닌 정수일 때 $C_n={}_{2n}\mathrm{C}_n \times \frac{1}{n+1}$인 수열로 정의된다.
위에서 쭉 했던 의미를 가지고 수열 $C$을 해석하면 $C_n$은 $(0, 0)$에서 $(n,n)$까지의 최단경로 중 다음 조건을 만족하는 경로의 개수이다.
- 이동 중 임의의 정수점까지 $x$축 방향으로 $n$번, $y$축 방향으로 $m$번 움직였다면 모든 정수점에 대해 $n \geq m$이 성립한다.
- 정수점만을 지난다.
'수학 > 경우의 수' 카테고리의 다른 글
| 카탈란 수의 점화식 (0) | 2021.09.24 |
|---|---|
| 분할과 분배 Pt. 2 (0) | 2021.04.12 |
| 분할과 분배 Pt.1 (0) | 2021.04.06 |
| 경우의 수 - 경로의 수 Pt. 1 (0) | 2020.12.17 |
| 경우의 수 - 순열과 조합 (0) | 2020.11.18 |
